Quick Tour -- MathMol
What is Molecular Modeling?
Molecular Modeling, is one of the fastest growing fields in science. It may vary from building and visualizing molecules (click image below for a short animation)...
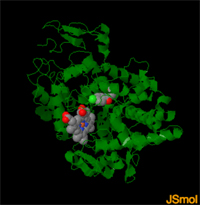
...to performing complex calculations on molecular systems. Below, molecular dynamics simulations are performed on a lipid-protein complex. Shown are the backbone structure of the protein, a bound fatty acid molecule within the protein, and a small shell of water surrounding the protein. The time for the simulation was 100 picoseconds. The graphs give information about the motion of the lipid inside the protein.
Why is Molecular Modeling Important?
By the time many of today's students enter the workforce, career opportunities will have radically changed. Most if not all of the 100,000 genes in the Human Genome will have been sequenced. Using molecular modeling scientists will be better able to design new and more potent drugs against diseases such as Cancer, AIDS, and Arthritis.
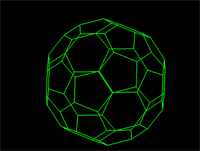
 5K ImageMolecular modeling not only has the potential to bring new drugs to the market, but a vast array of new materials. The discovery of fullerenes, and superconducting cuprates (as well as other complex inorganic compounds), are expected to produce new materials in the optics, ceramic, semiconductor and biomaterials markets.
5K ImageMolecular modeling not only has the potential to bring new drugs to the market, but a vast array of new materials. The discovery of fullerenes, and superconducting cuprates (as well as other complex inorganic compounds), are expected to produce new materials in the optics, ceramic, semiconductor and biomaterials markets.
 5K ImageIn addition, recent structural determination of vital photosynthetic proteins will lead the way to artificial photosynthesis.
5K ImageIn addition, recent structural determination of vital photosynthetic proteins will lead the way to artificial photosynthesis.
Why the Math in MathMol?
Numerous connections are found between mathematics and molecular modeling. Here are just a few!
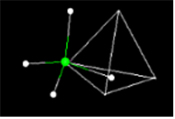
Many molecular structures have the same shape of familiar space figures. Take another look at the fullerene molecule shown above. The molecule has the same shape as an icosohedron. Notice that the faces are composed of hexagons and pentagons. The picture above shows another familiar space figure, that of the tetrahedron. Click on the picture and watch how the methane is superimposed onto the tetrahedron.
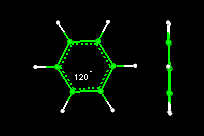
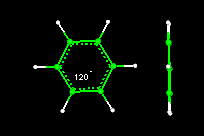
Angles are formed by the intersection of two rays (or line segments). The figure on the left shows a parallelogram with one base angle equal to 112 degrees. We measure angles formed by molecular bonds in a similar way, using three consecutive atoms to represent three points on a plane. The figure on the right shows the bond angle formed by 3 consecutive carbon atoms in a benzene ring.
Dihedral angles are formed by the intersection of two planes in space. On the left, two intersecting planes form a dihedral angle of 90 degrees. On the right, the dihedral angle shown for the hexane molecule is 59.4 degrees.
A line is a set of points described by an equation which may be written in the form y=mx+b where the constant m is the slope of the line and b represents its y intercept. As x varies y varies. In the figure above, as the temperature (T) of the system varies, the kinetic energy (E) of the molecule varies. The line describes the equation E=kT where k is the slope of the line.
The set of points which satisfy the equation y=1/x is a hyperbola. As x varies y varies inversely. As x becomes smaller y becomes larger. The movie above shows two particles of opposite charge attracted to each other. The relationship between coulombic energy and distance is an inverse relationship. The coulombic energy between the two particles varies with -1/r, where r is the distance separating their center of masses. In the movie notice that as r gets smaller, the potential energy becomes more negative.
The movie above shows that the torsion bond energy of a molecule can be modeled by a periodic function.
Many geometric figures display symmetry. The equilateral triangle on the left displays rotational symmetry. Rotating the figure about about a point formed by the intersection of the three angle bisectors (the incenter of the triangle) will give the same appearance. The ammonia molecule on the right also shows symmetry. It has a 3-fold axis of symmetry. Rotating the molecule 120 degrees about its axis will give the same appearance.
MATHMOL
- Activity 1: Measuring length and distance at the molecular level
- Activity 2: Geometry-of-1-Dimension
- Activity 3: Geometry of 2- Dimensions
- Activity 4: Geometry of 3-Dimensions
- Activity 5: Introduction to Molecular Modeling using Jsmol
- Activity 6: The Geometry of Crystals
- Activity 7: Summary Sheet by Students
- Activity 8: What is the Geometry of the Methane Molecule
- Activity 9: Geometry of the Crystal Structure of Ice
- Activity10:Geometry of the Benzene Molecule
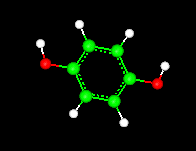 217K Movie
217K Movie 931K Movie
931K Movie 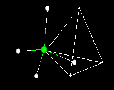 275K Movie
275K Movie
 5K Images
5K Images 
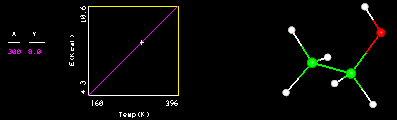 406K Movie
406K Movie 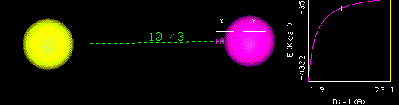 1066K Movie
1066K Movie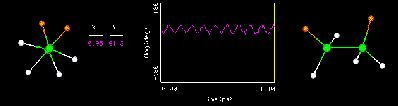 753K Movie
753K Movie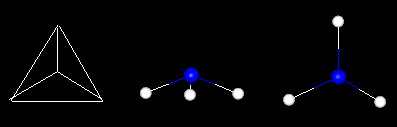 Image 5K
Image 5K