The Geometry of 2 Dimensions

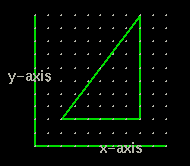
When we see a graph on a page we really don't think in terms of dimensions. But the graph above has only two axis or two dimensions. It is a plane.

Watch how the x-y graph rotates you can see it is a plane....

 

-------------->spin on -------->- spin off

---

Now look at the static graph below with the green axis. Each point is represented by an x and y position. To find the x-position we count to the right from the origin. To find the y-position we count up from the origin. Angle ABC is represented by three points.

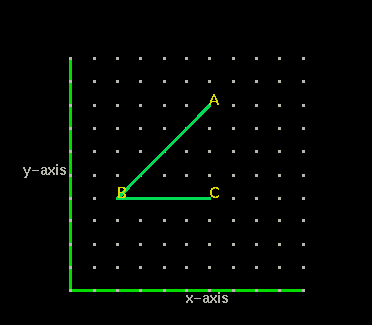
Point B has the coordinates (2,4). Starting from the origin (0,0) to reach point B we count 2 spaces to the right, then four spaces up.

What are the coordinates of point A?

What are the coordinates of point C?

---

-------------->spin on -------->- spin off

What type of triangle is shown above?

What is the measure of <ABC to the nearest tenth?

degrees

What is the sum of the three angles of the triangle equal to?

degrees.

Go to Geometry of 3-Dimensions

---