Geometry of 3-Dimensions

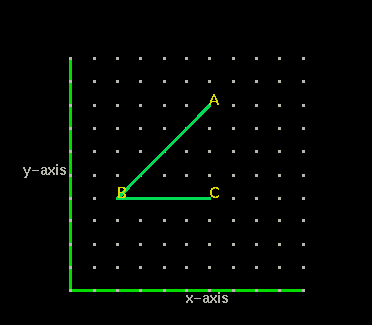
In the previous activity we saw a graph that showed <ABC on an x-y graph (see below). It was shown that the graph was a two dimensional plane.

The graph used the Cartesian coordinate system. The Cartesian coordinate system in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a coordinate axis or just axis (plural axes) of the system, and the point where they meet is its origin, at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. (see wikipedia for more about Cartesian coordinate system.

---

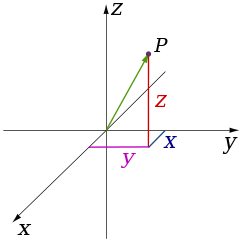
One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates . Below is shown the Cartesian coordinate system for 3-Dimensions. Note that the Z-axis points up.

 

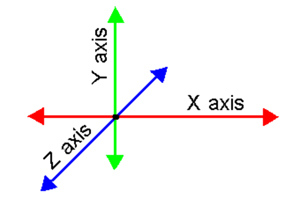
The Cartesian coordinate system with the Z-axis pointing up is what is taught in math and physics classes, However, different 3D tools ( animation and visual effect) smay have different directions for the Y and Z axis. Some 3D tools are Y-Up, which means the Y axis is a vertical line; while the others are Z-Up, means the Z axis is a vertical line. Y-Up is used in many video games and is also used in Jsmol which is being used in MathMol (see below -- image from Autodesk

---

Shown below is a cube using Jsmol app. In this system Y-is up and Z comes out of the plane.

-------------->spin on -------->- spin off

In Jsmol Y is up... By default the coordinate system is consistently right-handed, with +Y pointing up and + Z coming out of the screen.

You can measure line segments and angles the same way that was done in the 2-dimensions activity. For a line segment double click on first point, then drag to second point and double click again. To measure an angle, double click on point one drag to vertex click once, then drag to point 3 and double click.

Try these now:

What are the coordinates of point C?

What is the measure of <ABC to the nearest tenth?

degrees

---

What does all this have to do with molecules?

Molecules are solid 3 dimensional objects in 3 dimensional space. To describe molecules accurately we must describe their postion in 3-D space.

Look at the salt crystal structure below.. Each atom is represented on the x,y,z coordinate axis as a single ball.

-------------->spin on -------->- spin off
------>space fill/cpk -------->stick ----> ball-and-stick

To Rotate the Molecule--->Left Click and Drag

To Zoom-->>Left Click + hold Shift button and Drag Vertically

Jmol Menu --->>Right-Click

PDB File for Salt Molecule click here.

---